Thermophroesis as an emergent phenomenon: the role of internal states

• In our recent paper, we showed that thermophoresis can be an emergent phenomenon from chemical reaction systems. This blog is a lay summary of our work.

What is thermophoresis?

After establishing a temperature gradient in a solution system, we may observe the accumulation of solute particles on the cold or warm side. This phenomenon is known as thermophoresis. Its exact microscopic origin is still under debate. In our work¹, we propose a simple and intuitive mechanism to explain this phenomenon, which relies on the correlation of the energy-diffusion properties of the different states of the particles. It is based on a simple idea: particles stay longer where diffusion is slower, and temperature can modulate the transport property of particles.

The phenomenon of inhomogeneous concentration gradients driven by a temperature gradient.

From Einstein’s diffusion relation to thermophoresis

For the understanding of thermophoresis we can go back to the basic Einstein relation of diffusion:

The diffusion coefficient is proportional to the temperature divided by the damping constant, and the larger the particle the greater the damping (damping is proportional to particle size), which leads to an inverse relationship between diffusion coefficient and particle size as shown above.

Why do we mention the diffusion coefficient? Because the thermophoretic mechanism we propose here is rooted in nonhomogeneous diffusion and is simply based on a simple concept:

Particles tend to stay in the slow diffusion region for a longer time

This is quite intuitive idea. The diffusion process is essentially the random walk of microscopic particles, and where the random walk is slow, the particles will wander around for a longer time.

Then the emergence of thermophoresis is natural: the diffusion coefficient depends on temperature. Therefore, let’s look at the first term of Einstein’s relation, $\boxed{T}R^{-1}$. Isn’t it exactly the temperature? To put it more bluntly, this term tells us that particles diffuse faster in hot places and slower in cold places.

The temperature term in Einstein’s relation gives us a direct Soret coefficient:

However, there are two issues with this simple result.

1. This coefficient is always positive, which means that it can only indicate the tendency of accumulation in the cold region, namely the thermophoretic phenomenon. In contrast, it is observed experimentally that solute particles can move to the hot region.

2. This Soret coefficient is two orders of magnitude smaller than the experimentally measured values.

So we need to extract additional information from the Einstein relation. If we look at the Einstein relation again, $D\propto T R^{-1}$, there is a term related to the size of the particle, so can we derive thermophoresis from this term? The answer is yes, and this is the focus of our paper: chemical thermophoresis.

Chemical thermophoresis

To understand the thermophoresis from thermoresponsive particle size, we can start with a simple and intuitive example which is the foldable polymer

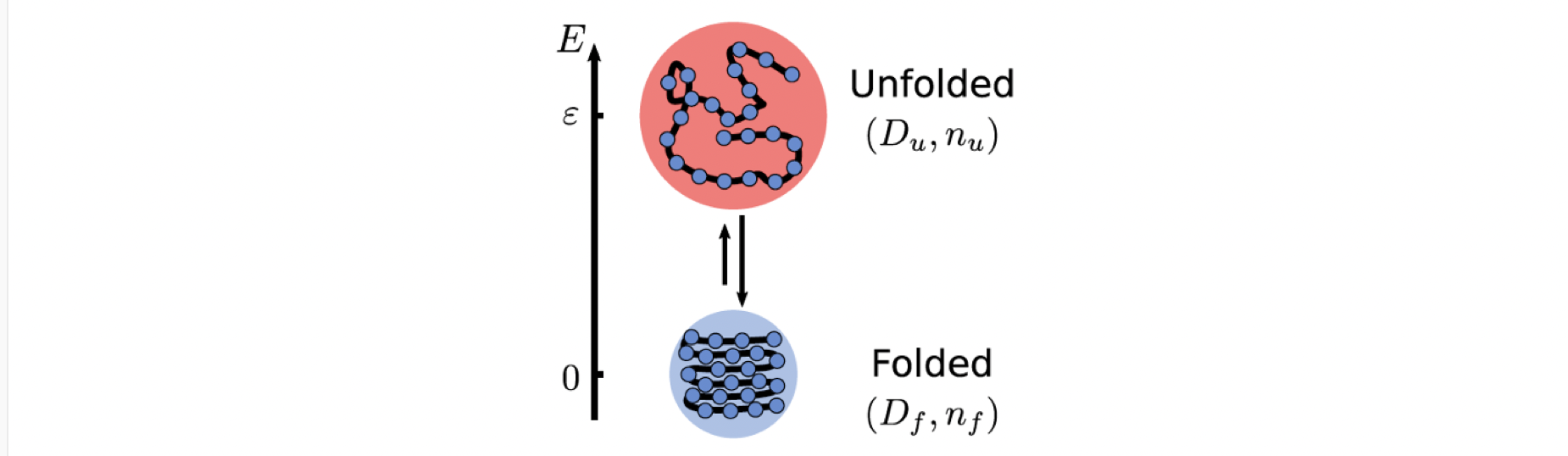Folded and unfolded states of a polymer.

A polymer can be in both folded and unfolded states. These two states have different free energies, taking into account the interactions between the various parts of the long chain and the interaction with the solvent molecules. Also, it is straightforward that the unfolded state of the polymer has a larger size. The Einstein relation tells us that particles of larger size encounter greater damping and diffuse more slowly. So, if temperature regulates the switching between these two states, we immediately have an average size that depends on temperature and thus a temperature-dependent effective diffusion coefficient.

And this temperature regulation is obvious, especially if we consider that the switching between unfolding and folding is reached fast enough in comparison to diffusion, the probability of being in each state is determined by the local temperature (local equilibrium approximation).

From the above Boltzmann distribution, which is the most fundamental law in thermodynamics, we can see that the probability of being in each state depends on the free energy of the state and the temperature of the local environment. Then, if we calculate the average, the effective diffusion coefficient is

which directly depends on the occupations in the two states, and the occupations are determined by the local temperature. Therefore, we have an effective diffusion coefficient that depends on the temperature.

To gain a better understanding, let’s consider the following limit: in the cold region, the particle is almost completely in the folded state, while in the hot region it is almost completely unfolded. The unfolded state in the hot region diffuses more slowly and thus leads to a negative Soret coefficient, which means that such a polymer can show thermophilic behavior.

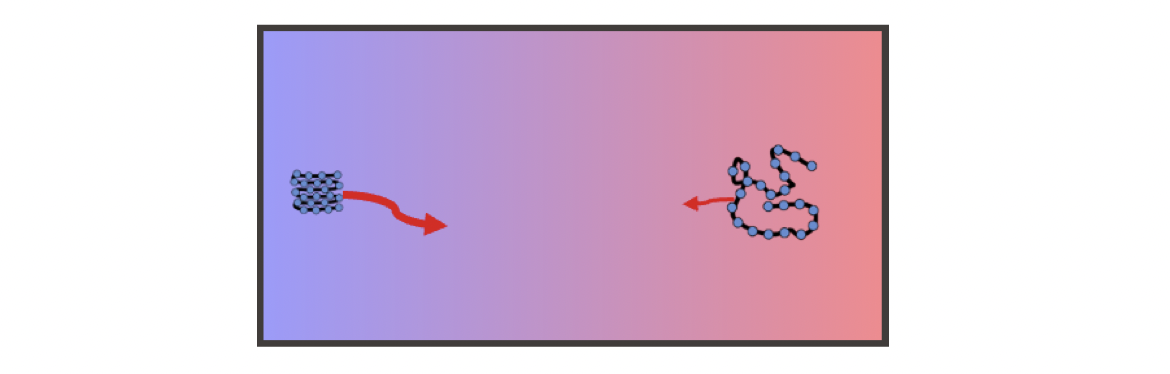Polymer can show thermophilic behavior.

Of course, in the limit case shown above, the always positive term, $S_T^0=1/T$, is not included. Overall, the thermophoresis of the particle depends on $D\propto \boxed{T}\boxed{R^{-1}}$ these two individual contributions. In the case of the example polymer, these two terms are positive and negative, respectively, which leads to the fact that the particle can switch from thermophobic to thermophilic as the temperature changes, i.e. the sign of the Soret coefficient changes. This positive and negative thermophoresis of polymers has been widely observed in experiments².

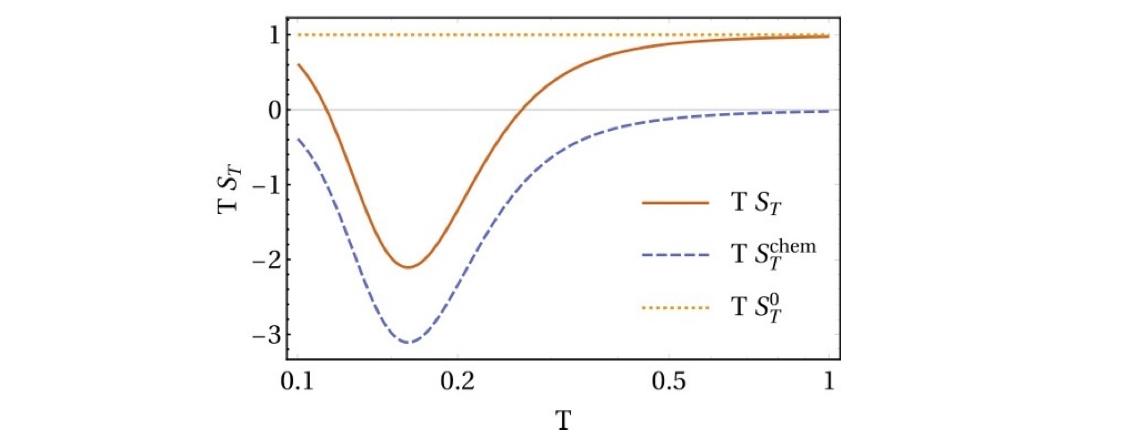The thermotropic and thermophilic behaviors of polymer be changed depending on the temperature.

Here $S_T^0=1/T$ is the contribution of the direct temperature-dependent term. While $S_T^\mathrm{chem}$ is what we call chemical thermophoresis, which originates from the thermoresponsive particle size.

For a more general case, we can consider that the particles have many internal states, which have different energies and diffusion coefficients. This energy-diffusion correlation leads to chemical thermophoresis. We can derive a very simple expression for the chemical Soret coefficient as

Here, the Soret coefficient is directly related to the covariance between the energies and the diffusion coefficients. If the energy and diffusion coefficients of the different states are positively correlated, we get a positive Soret coefficient, i.e. thermophobic, and vice versa, a more interesting thermophilic behavior.

Positive or negative chemical thermophoresis depends on the energy-diffusion correlation.

Complex chemical reactions

The chemical reactions covered in the previous section are the basic isomerization reactions, that is, no chemical complexes are formed. However, conceptually, it is straightforward to extend the chemical thermophoresis to more complex chemical reactions. For example, the following polymerization reaction

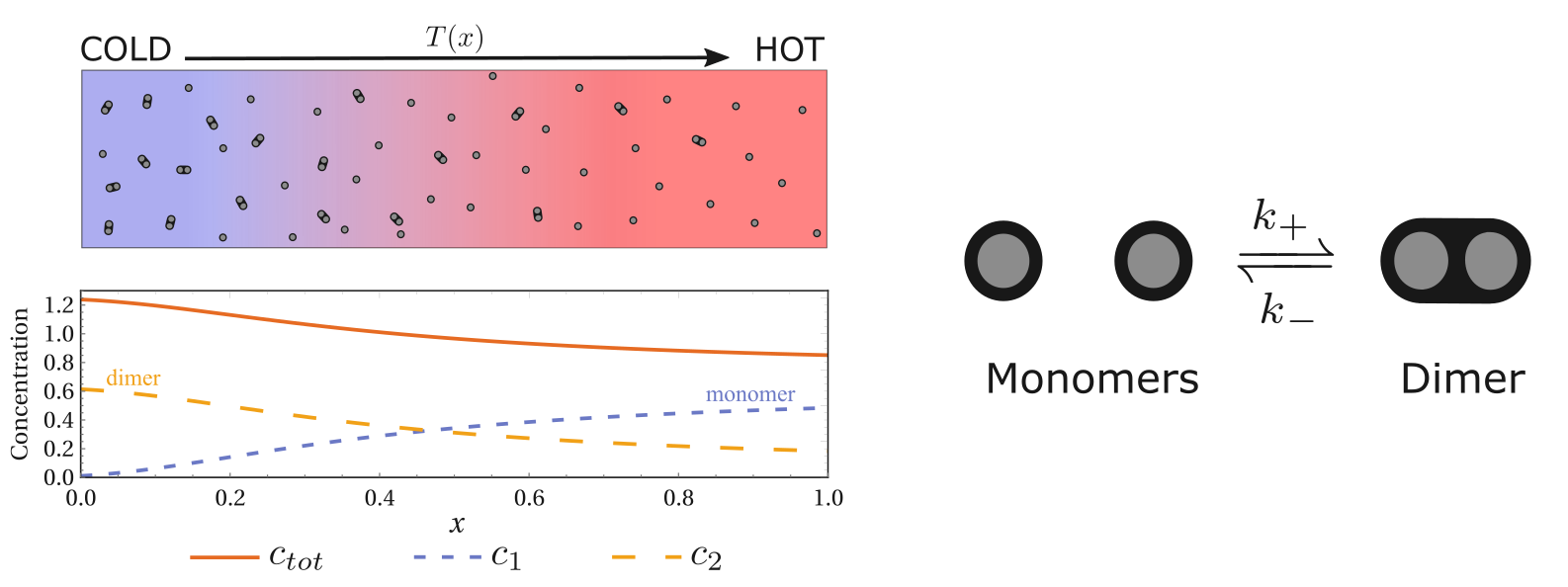Dimerization reaction can also exhibit thermophoresis.

Two monomers can form a dimer. Although the Soret coefficient derived from the previous isomerization cannot be directly applied, we can still use the energy-diffusion coefficient correlation to understand this thermophoretic phenomenon. Here, the energy and diffusion coefficients of the monomer and dimer are different, and as long as they are not the same, the system can respond to the temperature gradient and exhibit thermophoresis (inhomogeneous distribution) of the total concentration.

Discussion

Our theory gives a microscopic mechanism for the emergence of thermophoresis, which can be decomposed into several terms: the contribution of the temperature term of the Einstein relation itself, and the chemical thermophoresis as a consequence of energy-diffusion correlation. The actual thermophoretic phenomenon might be influenced by other mechanisms, such as those originating from the direct interaction of the particles with the solvent molecules³⁴. Therefore, the emergent chemical thermophoresis we discuss here may be the dominant term, but it may also be a small higher-order quantity that can be neglected. From our understanding, it is highly likely to observe chemical thermophoresis as the dominant mechanism when the structure of the particle is very sensitive to temperature change. For example, in PNIPAM systems, the folding and unfolding of the polymer exhibit phase transition with temperature, and “giant thermophoresis” can be measured at this phase transition point⁵⁶⁷. We expect that some experiments will be inspired to explore this direction.

Download the PDF

References