Three Fluctuation Theorems

class: centre, middle

## Three detailed fluctuation theorems$\ ^{[1]}$
#### *Shiling Liang*
 *Section of Physics, EPFL*
 
---

### Recap the fluctuation theorems

**Crooks fluctuation theorems**
$$
\frac{P(W)}{\bar{P}(-W)}=\exp\left[\beta(W-\Delta F)\right]
$$

**Jarzynski equality**

$$
\langle \exp(-\beta W)\rangle =\exp(-\beta \Delta F)
$$

> **constraints:** From one canonical equilibrium state to another equilibrium state with weak system-reservoir coupling.

**The most general form**
$$
\frac{P(\Delta S\_{tot})}{\bar{P}(-\Delta S\_{tot})}=\exp(\Delta S\_{tot})
$$

> Two choices of separation of entropy

>  - system + reservoir:  $S\_{tot}=S\_{s}+S\_{r}$

>  - adiabatic + non-adiabatic:  $S\_{tot}=S\_{a}+S\_{na}$ $\Rightarrow$ satisfy FT individually
---

### Detailed and integral fluctuation theorems

For a random variable $R$, it satisfies **integral fluctuation theorem** if

$$
\langle e^R\rangle=1
$$

and the **detailed fluctuation theorem**

$$
\exists \bar{P}\quad \frac{P(R)}{\bar{P}(-R)}=e^{R}\quad\forall R
$$

---

### Relative entropy/Kullback-Leibler distance
Kullback-Leibler distance characterize the difference between two probability distribution of (a) random variable(s) $\mathbf{m}$

$$
\mathcal{D}(P||\mathcal{\tilde{P}})=\sum\_mP\_\mathbf{m}\underbrace{\ln\frac{P\_\mathbf{m}}{\tilde{P}\_\mathbf{m}}}\_{\equiv r\_\mathbf{m}}
$$

One can verify that the random variable $r\_\mathbf{m}$ satisfies fluctuation theorem

$$
P(R)=\sum\_m\delta(R-r\_m)P\_m
$$
and

$$
\int dR\ P(R)e^{-R}=1
$$
---

### To physical systems

**Master equation (Markov process)**

$$
\dot{p}\_m(t)=\sum\_{m'}W\_{m.m'}(\lambda\_t)p\_{m'}(t)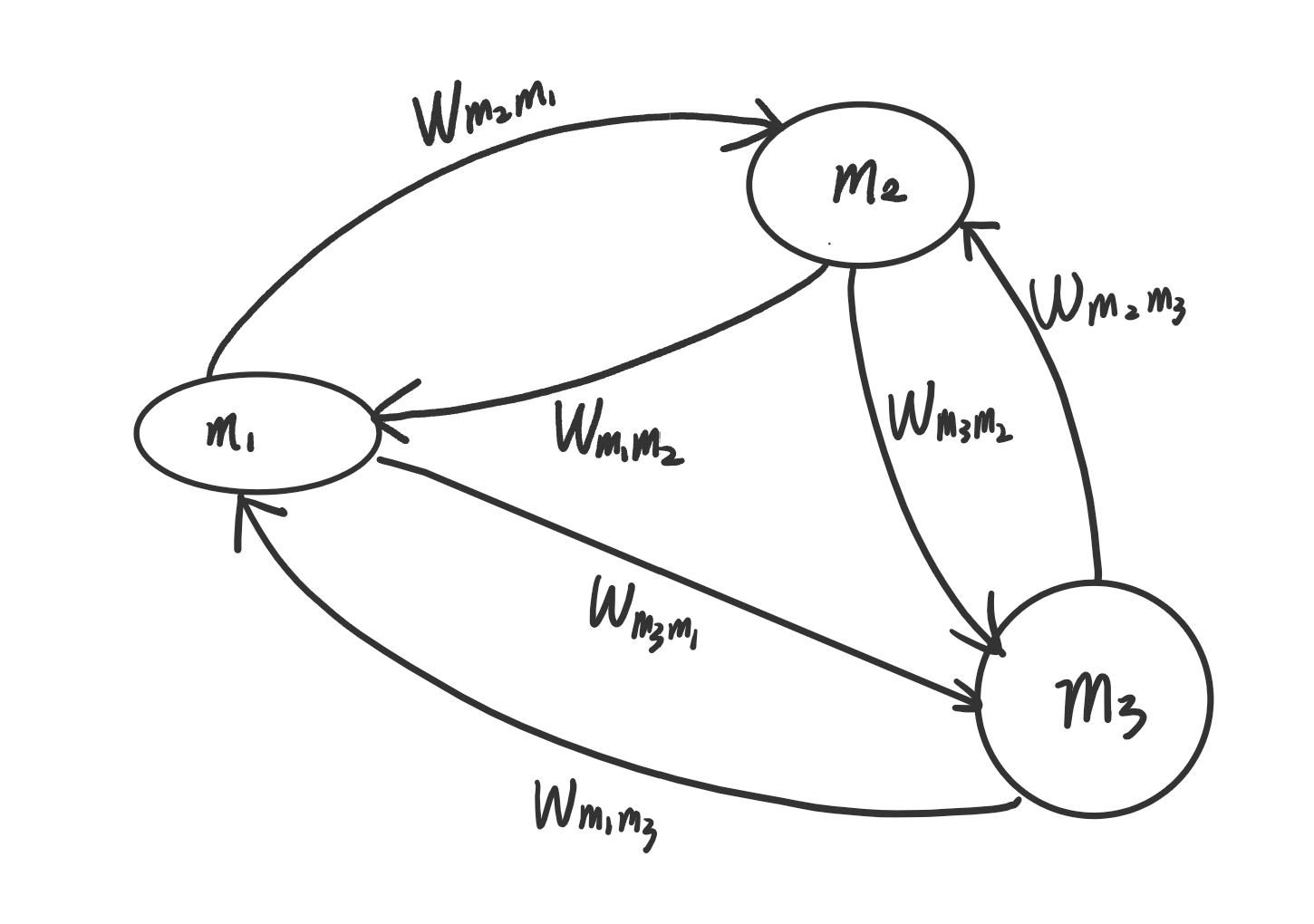
$$

---

**Probability of trajectories**

Now suppose we have a trajectory of random variables, $\mathbf{m}=\{m\_t,t\in [0,T]\}$, and discretized the time into $N$ steps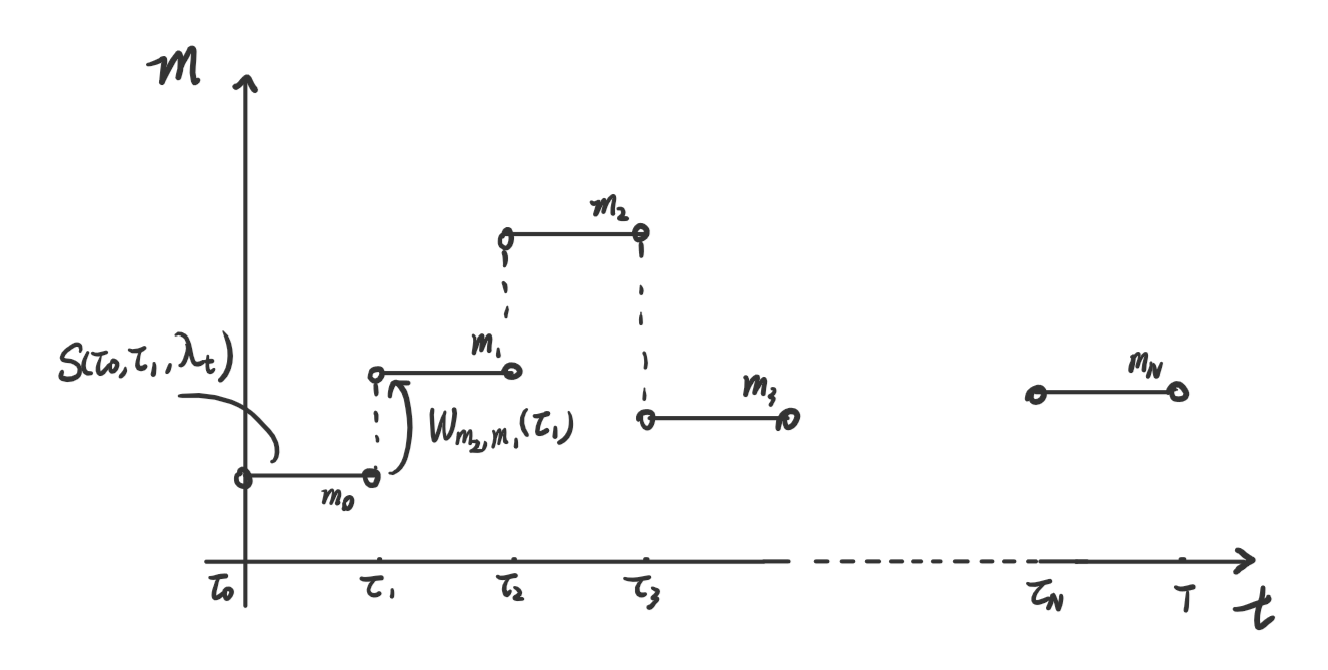 
![drawing](trajectory.png)

$$
\begin{equation}
\begin{aligned}
P\_\mathbf{m}
&=\prod\_{j=0}^Np\_{m\_j}(\tau\_j,\tau\_{j+1})\\\\
&=p\_{m\_0}(0)\left[\prod\_{j=1}^N S\_{m\_{j-1}}(\tau\_{j-1},\tau\_j,\lambda\_\tau)W\_{m\_j,m\_{j-1}}(\tau\_j)\right]S\_{m\_N}(\tau\_{N},T,\lambda\_\tau)\\\\
\end{aligned}
\end{equation}
$$

---
|![width75](trajectory.png)|
|:---:|
where $S\_{m\_{j-1}}(\tau\_{j-1},\tau\_j)$ is the survival probability

$$
S\_{m\_{j-1}}(\tau\_{j-1},\tau\_j,\lambda\_\tau)=\exp\left[\int\_{\tau\_{j-1}}^{\tau\_j}d\tau'\ W\_{m\_{j-1},m\_{j-1}}(\lambda\_{\tau'})\right]
$$

we can also write down the probability of the **reversed process**
$
\bar{\lambda}\_t=\lambda\_{T-t},\ \bar{m}\_j=m\_{N-j}
$

$$
\begin{aligned}
\bar{P}\_{\bar{m}}
&=\prod\_{j=0}^Np\_{\bar{m}\_{j}}(\tau\_{j},\tau\_{j+1})\\\\
&=p\_{m\_N}(T)\left[\prod\_{j=1}^N S\_{m\_j,m\_j}(\tau\_{j+1},\tau\_j,\bar{\lambda}\_{T-\tau})W\_{m\_{j-1},m\_j}\right]S\_{m\_0}(\tau,0,\bar{\lambda}\_{T-\tau})
\end{aligned}
$$

---

### Total entropy production

$$
\Delta S\_{tot}[\mathbf{m}]\equiv \ln\frac{P\_{\mathbf{m}}}{\bar{P}\_\mathbf{\bar{m}}}
$$

#### **system+reservoir picture**

$$
\Delta S\_{tot}[\mathbf{m}]=\underbrace{\ln\frac{p\_{m\_0}(0)}{p\_{m\_N}(T)}}\_{\text{system entropy}}+\underbrace{\sum\_{j=1}^N\ln\frac{W\_{m\_j,m\_{j-1}}(\lambda\_{\tau\_j})}{W\_{m\_{j-1},m\_j}(\lambda\_{\tau\_j})}}\_{\text{reservoir entropy}}
$$

#### **adiabatic+non-adiabatic picture**

$$
\Delta S\_{tot}[\mathbf{m}]=\underbrace{\ln\frac{p\_{m\_0}(0)}{p\_{m\_N}(T)}+\sum\_{j=1}^N\ln\frac{p\_{m\_j}^{st}(\lambda\_{\tau\_j})}{p\_{m\_{j-1}}^{st}(\lambda\_{\tau\_j})}}\_{\text{non-adiabatic }\Delta S\_{na}[\mathbf{m}]}
+\underbrace{\sum\_{j=1}^N\ln\frac{W\_{m\_j,m\_{j-1}}(\lambda\_{\tau\_j})p\_{m\_{j-1}}^{st}(\lambda\_{\tau\_j})}{W\_{m\_{j-1},m\_{j}}(\lambda\_{\tau\_j})p\_{m\_{j}}^{st}(\lambda\_{\tau\_j})}}\_{\text{adiabatic }\Delta S\_{a}[\mathbf{m}]}
$$

where $p\_m^{st}(\lambda\_t)$ is the steady state distribution, 
$
\sum\_{m'}W\_{m,m'}(\lambda\_t)p\_m^{st}(\lambda\_t)=0.
$

---
### Physical interpretations

If the system's stationary state satisfies detailed balance condition
$$
\frac{W\_{m,m'}(\lambda\_t)}{W\_{m',m}(\lambda\_t)}=\frac{p\_m^{st}(\lambda\_t)}{p\_{m'}^{st}(\lambda\_t)}\quad\forall m,m'
$$
the adiabatic contribution is zero
$$
\Delta S\_{a}[\mathbf{m}]=0\Rightarrow \Delta S\_{tot}[\mathbf{m}]=\Delta S\_{na}[\mathbf{m}]
$$

If the relaxation process is much faster than the time scale of the schedule $\lambda\_t$, i.e. quasi-static process

$$
\langle\Delta S\_{na}[\mathbf{m}]\rangle=0 \Rightarrow \Delta S\_{tot}[\mathbf{m}]=\Delta S\_{a}[\mathbf{m}]
$$

---
### Examples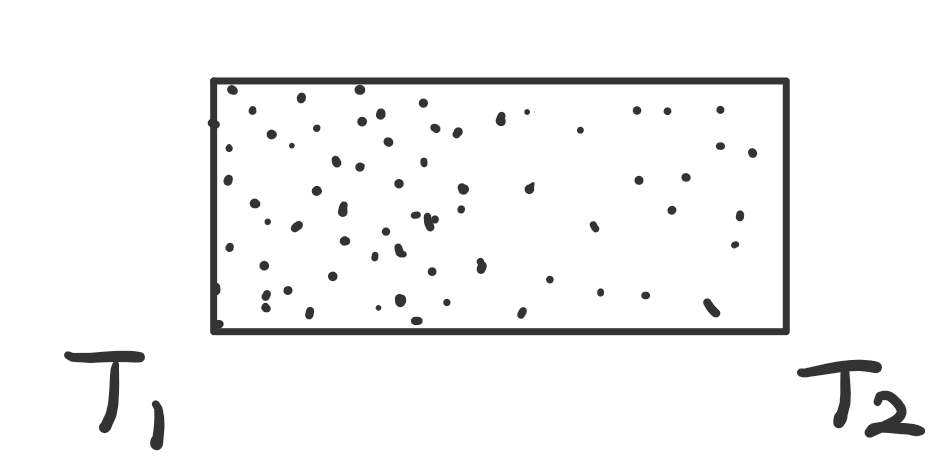

|![half](adiabatic.png)|
|:---:|
|**Fig.** Non-equilibrium steady state, $\Delta S\_{a}\neq 0$|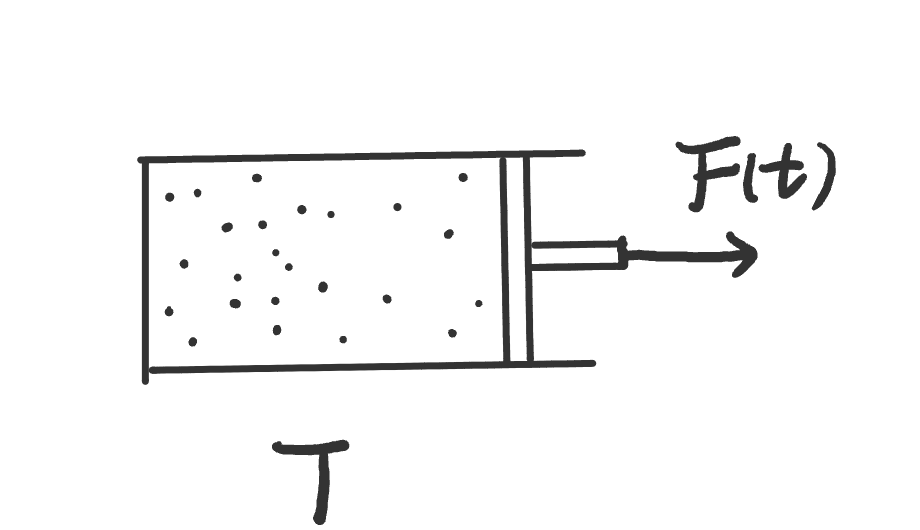

|![half](non-adiabatic.png)||
|:---:|
|**Fig.** The external force varies faster than the relaxation of the system, $\langle\Delta S\_{na}\rangle\neq 0$|

---

### Three fluctuation theorems

By introducing the adjoint transition matrix $\mathbf{W}^+$

$$
W\_{m,m'}^+=\frac{W\_{m',m}(\lambda\_t)p\_m^{st}(\lambda\_t)}{p\_{m'}^{st}(\lambda\_t)}
$$

one can obtain the following relation

$$
\Delta S\_{na}[\mathbf{m}]\equiv\ln\frac{P\_\mathbf{m}}{\bar{P}\_{\mathbf{\bar{m}}}^+},\quad \Delta S\_a[\mathbf{m}]\equiv\frac{P\_{\mathcal{m}}}{P\_{\mathbf{m}}^+}
$$

Using the mathematical relation we introduced before, one can obtain three detailed fluctuation theorems

$$
\frac{P(\Delta S\_{tot})}{\bar{P}(-\Delta S\_{tot})}=e^{\Delta S\_{tot}}
$$

$$
\frac{P(\Delta S\_{na})}{\bar{P}^+(-\Delta S\_{na})}=e^{\Delta S\_{na}},\quad 
\frac{P(\Delta S\_{a})}{P^+(-\Delta S\_{a})}=e^{\Delta S\_{a}}
$$

---
### Reference

[1] Esposito, M. and Van den Broeck, C., 2010. Three detailed fluctuation theorems. Physical review letters, 104(9), p.090601.

---
.center[#Thanks]